问题
填空题
若(x+1)8=a0+a1x+a2x2+…+a8x8,则a0+a2+a4+a6+a8的值为______.
答案
∵(x+1)8=a0+a1x+a2x2+…+a8x8,令x=1可得 28=a0+a1+a2+a3+…+a8.
再令x=-1可得 0=a0-a1+a2-a3+…+a8.
两式相加可得 28=2(a0+a2+a4+a6+a8),∴a0+a2+a4+a6+a8 =27=128,
故答案为128.
若(x+1)8=a0+a1x+a2x2+…+a8x8,则a0+a2+a4+a6+a8的值为______.
∵(x+1)8=a0+a1x+a2x2+…+a8x8,令x=1可得 28=a0+a1+a2+a3+…+a8.
再令x=-1可得 0=a0-a1+a2-a3+…+a8.
两式相加可得 28=2(a0+a2+a4+a6+a8),∴a0+a2+a4+a6+a8 =27=128,
故答案为128.
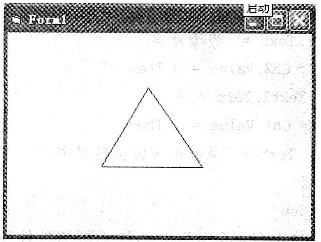
在名称为Form1的窗体上画出如阿所示的三角形。
下表给出了直线Line1、Line2的坐标值,请按此表画Line1、 Line2,并画出直线Line3,从而组成如图所示的三角形。
| 表Line1、Line2的坐标值
|