问题
问答题
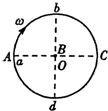
如图所示,按顺时针方向在竖直平面内作匀速转动的轮子边缘上有一点A.当A通过与圆心等高的a点时,有一质点B从圆心O开始做自由落体运动.已知圆的半径为R,求:
(1)轮子的角速度ω满足什么条件时,点A才能与B相遇?
(2)轮子的角速度ω满足什么条件时,点A与B的速度才会相同?
答案
(1)质点从B点做自由落体运动,根据R=
gt2得:1 2
t=2R g
A和B只能在d点相遇,所以A运动的时间为(n+
)T,3 4
所以(n+
)T=(n+3 4
)3 4
=2π ω
(n=0,1,2…)2R g
解得:ω=2π(n+
)3 4
(n=0,1,2…)g 2R
(2)点A与B的速度相同的位置只能在c点,
则t=(n+1)T,
根据速度相等有:ωR=gt=g(n+1)
(n=0,1,2…)2π ω
解得:ω=
(n=0,1,2…)2πg(n+1) R
答:(1)轮子的角速度ω=2π(n+
)3 4
(n=0,1,2…)时,点A才能与B相遇;g 2R
(2)轮子的角速度ω=
(n=0,1,2…)时,点A与B的速度才会相同.2πg(n+1) R
