如图所示,矩形区域MNPQ内有水平向右的匀强电场,虚线框外为真空区域;半径为R、内壁光滑、内径很小的绝缘半圆管ADB固定在竖直平面内,直径AB垂直于水平虚线MN,圆心O恰在MN的中点,半圆管的一半处于电场中.一质量为m,可视为质点的带正电电荷量为q的小球从半圆管的A点由静止开始滑入管内,小球从B点穿出后,能够通过B点正下方的C点.重力加速度为g,小球在C点处的加速度大小为5g/3.求:
(1)匀强电场场强E;
(2)小球在B点时,半圆轨道对它作用力的大小;
(3)要使小球能够到达B点正下方C点,虚线框MNPQ的高度和宽度满足什么条件;
(4)小球从B点计时运动到C点过程中,经多长时间小球的动能最小.
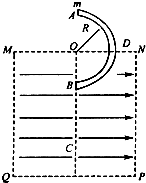
(1)由于小球在C处受到重力和电场力的共同作用,所以:
C点:F合=ma=(qE)2+m2g2
代入数据得:E=4mg 3q
(2)A→B的过程重力和电场力对小球做功,mg•(2R)-FR=
mvB21 2
得:vB=4gR 3
在B点N-mg=mvB2 R
半圆轨道对小球的作用力 N=
mg7 3
(3)小球从B→C 水平方向匀减速运动,竖直方向自由落体运动
ax=
gay=g4 3
设向左减速时间为tt=
=vB ax 3R 4g
x=
vBt=1 2 R 2
y=
g(2t)2=1 2 3R 2
宽度应满足条件L>2R,
高度满足条件H≥
R5 2
(4)当F与mg的合力与v垂直时,小球的动能最小,设经过的时间为t∴vy=
vxvy=gtvx=vB-4 3
gt4 3
∴t=8 25 3R g
答:(1)匀强电场场强E=
;4mg 3q
(2)小球在B点时,半圆轨道对它作用力的大小N=
mg;7 3
(3)要使小球能够到达B点正下方C点,虚线框MNPQ的高度和宽度满足H≥
R;5 2
(4)小球从B点计时运动到C点过程中,经t=8 25
时间小球的动能最小.3R g
