问题
填空题
我们常用构造等式对同一个量算两次的方法来证明组合恒等式,如由等式(1+x)2n=(1+x)n(1+x)n可得,左边xn的系数为
利用上述方法,化简(
|
答案
根据题意,构造等式(x-1)2n•(x+1)2n=(x2-1)2n,
由等式的左边可得x2n的系数为C2n2n•(-1)2nC2n0+C2n2n-1•(-1)2n-1C2n1+C2n2n-2•(-1)2n-2C2n2+…+C2n0•(-1)0C2n2n,
即(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2,
由右等式的右端可得 x2n的系数为(-1)nC2nn,
故有(C2n0)2-(C2n1)2+(C2n2)2-(C2n3)2+…+(C2n2n)2=(-1)nC2nn,
故答案为(-1)nC2nn.

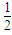 mgtgθ
mgtgθ mgsinθ
mgsinθ