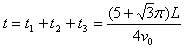问题
计算题
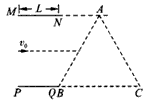
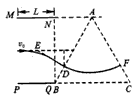
两块平行金属板MN、PQ水平放置，板长为L，两板间距离为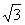
L。在紧靠平行板右侧的正三角形区域内存在着垂直于纸面的匀强磁场，三角形底边BC与PQ在同一水平线上，顶点A与MN在同一水平线上，如图所示。一个质量为m、电荷量为+q的粒子沿两板间中心线以初速度v0水平射入，若在两板间加某一恒定电压，粒子离开电场后恰好垂直于AB边进入磁场，并垂直于AC边射出。不计粒子的重力，整个装置都处于真空中。求：
（1）两极板间的电压的大小；
（2）三角形区域内的磁感应强度的大小；
（3）粒子从开始进入电场到从AC边射出经历的时间。
答案
解：（1）运动的水平位移L=v0t1
分解电场中类平抛的末速度可得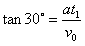
由牛顿第二定律得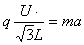
解得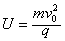
（2）粒子运动的轨迹如图所示
磁场中，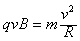
，即
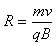
由几何关系可确定半径AD长度为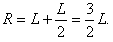
进入磁场的速度v满足v0=vcos30°
解得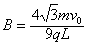
（3）粒子在电场中的偏转时间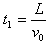
粒子飞出电场到刚要进磁场的过程中做匀速直线运动，这个过程位移的水平分量为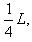
所用时间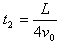
粒子在磁场中的运动时间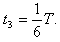
而运动周期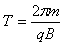
，解得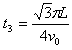
所以总的运动时间为