小明调查了他们班50名同学各自家庭的人均日用水量(单位:升),结果如下:
55 42 50 48 42 35 38 39 40 51 47 52 50 42 43 47 52 48 54 52 38 42 60 52 41 46 35 47 53 48 52 47 50 49 57 43 40 44 52 50 49 37 46 42 62 58 46 48 39 60
请根据以上数据绘制频数分布表和频数分布直方图,并回答下列问题:
(1)家庭人均日用水量在哪个范围的家庭最多?这个范围的家庭占全班家庭的百分之几?
(2)家庭人均日用水量最少和最多的家庭各占全班家庭的百分之几?
(3)如果每人每天节约用水8升,按全班50人计算,一年(按365天计算)可节约用水多少吨?按生活基本日均需水量50升的标准计算,这些水可供1个人多长时间的生活用水?
这组数据中最大值是62,最小值是35,它们的差是27.若取组距为4,由于27÷4≈7,因此要将整个数据分为7组,用x(升)表示人均日用水量,则所分的组为35≤x<39,39≤x<43,43≤x<47,59≤x<63.整理可得下列频数分布表:
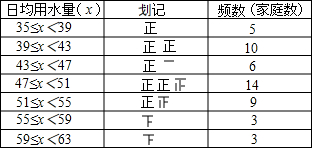
用横轴表示人均日用水量,等距离标出各组的端点35、39、43、63,用纵轴表示频数,等距离标出3、6、9、12、15等,以各组的频数为高画出与这一组对应的长方形,得到频数分布直方图(如图)根据频数分布表和频数分布直方图可以得到:
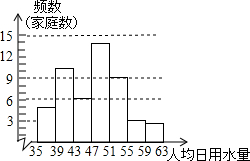
(1)家庭人均日用水量在不小于47升而小于51升的范围内的家庭最多,这个范围内的家庭共有14家,
占全班家庭的百分比
×100%=28%.14 50
(2)家庭人均日用水量最少和最多的家庭分别占全班家庭的10%和6%.
(3)一天可节约用水:8×50×365÷1000=146(吨),
按生活基本日均需水量50升的标准计算,这些水可供1个人生活:146×1000÷50÷365=8(年).
