问题
计算题
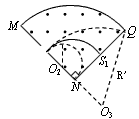
如图，离子源A产生的初速为零、带电量均为e、质量不同的正离子被电压为U0的加速电场加速后匀速通过准直管，垂直射入匀强偏转电场，偏转后通过极板HM上的小孔S离开电场，经过一段匀速直线运动，垂直于边界MN进入磁感应强度为B的匀强磁场。已知HO＝d，HS＝2d，∠MNQ＝90°。（忽略粒子所受重力）
（1）求偏转电场场强E0的大小以及HM与MN的夹角φ；
（2）求质量为m的离子在磁场中做圆周运动的半径；
（3）若质量为4m的离子垂直打在NQ的中点S1处，质量为16m的离子打在S2处。求S1和S2之间的距离以及能打在NQ上的正离子的质量范围。
答案
解：（1）正离子被电压为U0的加速电场加速后速度设为V1，设对正离子，应用动能定理有
eU0＝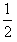
mV12
正离子垂直射入匀强偏转电场，作类平抛运动
受到电场力F＝qE0、产生的加速度为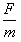a＝
，即a＝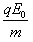
垂直电场方向匀速运动，有2d＝V1t
沿场强方向：Y＝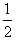
at2
联立解得E0＝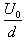
又tanφ＝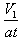
解得φ＝45°
（2） 正离子进入磁场时的速度大小为V2＝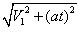
，正离子在匀强磁场中作匀速圆周运动，由洛仑兹力提供向心力，qV2B＝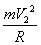
解得离子在磁场中做圆周运动的半径R＝2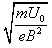
（3）根据R＝2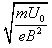
可知
质量为4m的离子在磁场中的运动打在S1，运动半径为R1＝2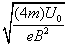
质量为16m的离子在磁场中的运动打在S2，运动半径为R2＝2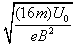
又ON＝R2－R1
由几何关系可知S1和S2之间的距离ΔS＝
－R1
联立解得ΔS＝4(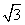
－)
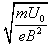
由R′2＝(2R1)2+(R′－R1)2，解得R′＝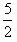
R1
再根据
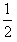R1＜R＜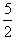
R1，解得m＜mx＜25m
