问题
填空题
已知AB是异面直线a、b的公垂线段,AB=2,且a与b成30°角,在直线a上取AP=4,则点P到直线b的距离为______.
答案
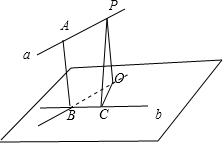
过B作直线c,c∥a,过P作PO垂直于c,垂足为O,
过O作OC⊥b垂足为C,
∵AB是异面直线a、b的公垂线段,∴AB⊥α,AB∥PO,∴PO⊥α,
根据三垂线定理,PC⊥b.
PC长为点P到直线b的距离.
OC=4×cos30°=2,PO=AB=2,
在Rt△OCP中,
PC=
=PO2+OC2
=24+4 2
故答案是2
.2
