问题
填空题
在矩形ABCD中,AB=2,BC=1,取AB中点E,CD中点F,若沿EF将矩形AEFD折起,使得平面AEF⊥平面EFB,则AE中点Q到平面BFD的距离为______.
答案
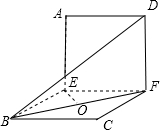
取BF中点O,连接EO,则EO⊥BF
∵平面AEF⊥平面EFB,平面AEF∩平面EFB=EF,DF⊥EF
∴DF⊥平面EFB
∵EO?平面EFB
∴DF⊥EO
∵DF∩BF=F
∴EO⊥平面BFD
∵AE∥DF,AE?平面BFD,DF?平面BFD
∴AE∥平面BFD
∴AE中点Q到平面BFD的距离等于E到平面BFD的距离,即EO
由题意,EFCB是正方形,∴EO=2 2
即AE中点Q到平面BFD的距离等于2 2
故答案为:2 2
