边长为a的正六边形ABCDEF在平面a内，PA⊥a，PA=a，则P到CD的距离为_爱下问搜题

搜题请搜索小程序“爱下问搜题”

问题填空题

边长为a的正六边形ABCDEF在平面a内，PA⊥a，PA=a，则P到CD的距离为______，P到BC的距离为______．

答案

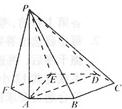
连接AC，CD⊥AC

∵PA⊥平面a，CD?平面a

∴PA⊥CD，而PA∩AC=A

∴CD⊥平面PAC，则PC⊥CD

在直角三角形PAC中，AC=

3

a，PA=a，

根据勾股定理可知PC=2a

即P到CD的距离为2a；

过点A作BC的垂线交BC的延长线于点Q，连接PQ

在直角三角形PAQ中，AQ=

3

2

a，PA=a

根据勾股定理可知PQ=

7

2

a

∴P到BC的距离为

7

2

a

故答案为：2a，

7

2

a

多项选择题

维果斯基认为心理机能由低级向高级发展的标志是( )。

A．心理活动的随意机能

B．心理活动的抽象一概括机能

C．形成以符号或词为中介的心理结构

D．心理活动的个性化

填空题

放大电路应遵循的基本原则是：（）结正偏；（）结反偏。