问题
选择题
已知AB是异面直线a,b的公垂线段,AB=2,且a与b成30°角,在直线a上取AP=4,则点P到直线B的距离为( )
|
答案
过点B作直线BM∥a,过点P作MP⊥BM,过点M作MN⊥BN,连接PN,如图所示:
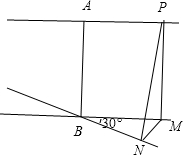
由以上可得:AB∥PM,AB=PM,所以AP=BM.
所以PM⊥平面BNM,
所以BN⊥MN,BN⊥PM,
所以BN⊥平面PMN,可得BN⊥PN,所以PN为点P到直线b的距离.
因为AP=4,所以BM=4.
因为∠MBN=30°,所以MN=2,
又因为PM=2,所以PN=2
.2
故选A.
