问题
填空题
已知三棱锥P-ABC中,△ABC是边长为3的等边三角形,侧棱长都相等,半径为2的球O过三棱锥P-ABC的四个顶点,则PA=______.
答案
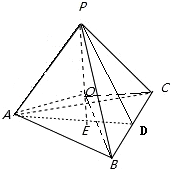
根据题意,三棱锥P-ABC是正三棱锥,设P在底面的射影是E
延长AE交BC于D,连接PD、OA、OB、OC
∵,△ABC是边长为3的等边三角形,
∴AE=
AB=3 3
,DE=3 3 6
∵半径为2的球O过三棱锥P-ABC的四个顶点,
∴球心O在PE上,设OE=x
则AO=
=2,得(AE2+OE2
)2+x2=4,解得x=1(舍负)3
∴PE=PO±OE=1或3
因此,Rt△PAE中,PA=
=2或2AE2+PE2 3
故答案为:2或23