问题
问答题
设
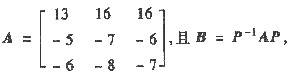
(Ⅰ) 求矩阵A的特征值与特征向量;
(Ⅱ) 当
 时,求矩阵B;
时,求矩阵B;
(Ⅲ) 求A100.
答案
参考答案:(Ⅰ) 由矩阵A的特征多项式
[*]
得矩阵A的特征值λ1=λ2=1,λ3=-3.
由齐次线性方程组(E-A)x=0,[*]
得基础解系 η1=(-4,1,2)T.
由齐次方程组(-3E-A)x=0,[*]
得基础解系 η2=(-2,1,1)T.
因此,矩阵A关于特征值λ1=λ2=1的特征向量为k1(-4,1,2)T,k1≠0;
而关于特征值λ=-3的特征向量为k2(-2,1,1)T,k2≠0.
(Ⅱ) [*]
(Ⅲ) 由p-1AP=B有p-1A100P=B100,故A100=PB100P-1.又B100=[*],
于是[*]
[*]
