问题
选择题
在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )
|
答案
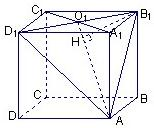
如图,设A1C1∩B1D1=O1,∵B1D1⊥A1O1,B1D1⊥AA1,∴B1D1⊥平面AA1O1,
故平面AA1O1⊥面AB1D1,交线为AO1,在面AA1O1内过B1作B1H⊥AO1于H,
则易知A1H的长即是点A1到截面AB1D1的距离,在Rt△A1O1A中,A1O1=
,2
AO1=3
,由A1O1•A1A=h•AO1,可得A1H=2
,4 3
故选:C.
