问题
填空题
（理）已知三条线段PA，PB，PC两两垂直，底面ABC内一点Q到三个面PAB、PBC、PCA的距离分别为
|
答案
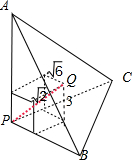
由题意如图，
三条线段PA，PB，PC两两垂直，底面ABC内一点Q到三个面PAB、PBC、PCA的距离分别为
、 3 、 2
，6
为棱扩展为长方体，求出体对角线的长，就是Q点与顶点P之间的距离．
所以PQ=
=(
)2+32+(2
)26 17
故答案为：
．17
搜题请搜索小程序“爱下问搜题”