问题
填空题
过点M0(1,-2,0)且与直线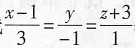 垂直的平面方程为().
垂直的平面方程为().
答案
参考答案:3(x-1)-(y+2)+z=0(或3x-y+z=5)
解析:
[解题指导] 本题考查的知识点为平面与直线的方程.
由题设条件可知应该利用点法式方程来确定所求平面方程.
所给直线l的方向向量s=(3,-1,1).若所求平面π垂直于直线l,则平面π的法向量n∥s,不妨取n=s=(3,-1,1).则由平面的点法式方程可知
3(x-1)-[y-(-2)]+(z-0)=0,
即 3(x-1)-(y+2)+z=0
为所求平面方程.
或写为 3x-y+z-5=0.
上述两个结果都正确,前者3(x-1)-(y+2)z=0称为平面的点法式方程,而后者3x-y+z-5=0称为平面的一般式方程.
