问题
选择题
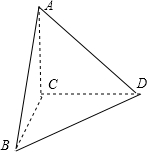
在三棱锥A-BCD中,AC⊥底面BCD,BD⊥DC,BD=DC,AC=a,∠ABC=30°,则点C到平面ABD的距离是( )
|
答案
∵AC⊥平面BCD,BC、BD⊂平面BCD,
∴AC⊥BC,BD⊥AC,
∵BD⊥DC,AC∩CD=D,
∴BD⊥平面ACD,
∵AD⊂平面ACD,
∴BD⊥AD,
∴△ABD是直角三角形,
∵AC=a,∠ABC=30°,
∴AB=2AC=2a,BC=
a,3
∵△DBC是等腰直角三角形,
∴BD=CD=
BC=2 2
a,6 2
∴S△BCD=
×BD×CD=1 2
a2,3 4
∵AD=
=AB2-BD2
a,10 2
∴S△ABD=
×AD×BD=1 2
a2,15 4
设C到平面ABD距离为d,
由VC-ABD=VA-BCD,可得
×1 3
a2×d=15 4
×1 3
a2×a3 4
∴d=
a.15 5
故选B.
