问题
问答题
已知流体从容器中流出的速度
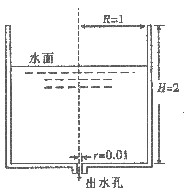
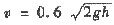(米/秒)，其中重力加速度g=10米/秒2，h为流体表面在开口孔上方的高度(单位：米)．现有盛满水的半径R=1米，高度H=2米的直立的圆柱形水箱，在圆柱形水箱的底部有一个半径r=0.01米的小圆孔，水箱的剖面图如右图．求水箱中的水经过底部小圆孔全部流尽所需的时间．
答案
参考答案：以水箱底部小孔中心为坐标原点，以圆柱形水箱的圆柱中心轴为h轴，且h轴的正向指向上方，建立如图的坐标系．设水箱中的水从其底部小孔开始流出的时刻为t=0，并从此时刻开始计时，时间单位为秒．于是当t=0时水箱中的水深度h(0)=2(单位：米)．
[*]
设时刻t水箱中水的深度为h(t)，则从时刻t到t+dt，从水箱底部小孔流出的水的体积
[*]
若水箱中的水位相应下降dh，则dh与dV满足
-dV=πR2dh．
由此即得微分方程
[*]
为了计算水箱中的水从其底部小孔全部流尽所需的时间T，只要把以上方程两端分别积分，其中左端是从t=0到t=T求积分，而右端则是从h(0)=2到h(T)=0求积分．于是
[*]