问题
解答题
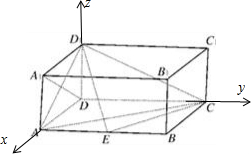
在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:A1D∥平面BCC1B1;
(2)当E为AB的中点时,求点E到面ACD1的距离.
答案
(本题满分14分)
(1)连接B1C,因为几何体是长方体,
所以A1B1CD是矩形,所以A1D∥B1C,
因为B1C⊂平面平面BCC1B1,A1D⊄平面BCC1B1,
所以A1D∥平面BCC1B1;
(2)建立如图的坐标系,
=(1,0,1),DA1
此时,E(1,1,0),
=(1,1,-1),D1E
设平面ACD1的法向量是
=(1,x,y),n
=(-1,2,0),AD1
由
• n
=0,AD1
•n
=0,得AC
=(1,n
,1),1 2
取
=(2,1,2),n
点E到面ACD1的距离d=
=|
•n
|D1E |
|n
.1 3
