问题
填空题
已知球O的半径为1，A，B，C三点都在球面上，且每两点间的球面距离为
|
答案
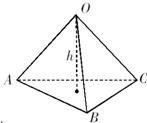
球心O与A，B，C三点构成正三棱锥O-ABC，如图所示，
已知OA=OB=OC=R=1，∠AOB=∠BOC=∠AOC=90°，
由此可得AO⊥面BOC．
∵S△BOC=
，S△ABC=1 2
．3 2
∴由VA-BOC=VO-ABC，得h=
．3 3
故答案为：3 3
搜题请搜索小程序“爱下问搜题”
已知球O的半径为1，A，B，C三点都在球面上，且每两点间的球面距离为
|
球心O与A，B，C三点构成正三棱锥O-ABC，如图所示，
已知OA=OB=OC=R=1，∠AOB=∠BOC=∠AOC=90°，
由此可得AO⊥面BOC．
∵S△BOC=
，S△ABC=1 2
．3 2
∴由VA-BOC=VO-ABC，得h=
．3 3
故答案为：3 3