搜题请搜索小程序“爱下问搜题”
问题 解答题

已知正方体ABCD-A1B1C1D1的棱长是1，求直线DA1与AC间的距离．

答案

建立如如图所示坐标系，则A（0，0，0），C（1，1，0），D（0，1，0），

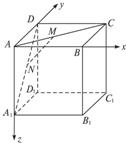
A1（0，0，1），

AC
=（1，1，0），
DA1
=（0，-1，1），

设MN为直线DA1与AC的公垂线段，且

MN
=（x，y，z），

且

MN
⊥
AC
，
MN
⊥
DA1
，x+y=0，-y+z=0，令y=t，则
MN
=（-t，t，t），

而另可设M（m，m，0），N（0，a，b），则

MN
=（-m，a-m，b），

∴

-m=-1
a-m=t
b=t.
∴N（0，2t，t）．

又2t+t=1，∴t=

1
3
．

∴

MN
=（-
1
3
，
1
3
，
1
3
，|
MN
|=
1
9
+
1
9
+
1
9
=
3
3
．

即直线DA1与AC间的距离为

3
3
．

多项选择题 案例分析题

患者女，25岁。足月妊娠G1P0，因近2周持续性头痛头昏、双下肢浮肿，入院待产。患者在病房能缓慢行走，既往无心脏病、高血压病史。体格检查：意识清楚、血压160/120mmHg、心率82次／分、双下肢浮肿（++）；实验室检查：Hb98g/L、血总蛋白47.3gL、尿蛋白（++）、PT13.4s、APTT38.2s、血小板159×109/L、血电解质及血糖正常。

决定立即剖宫产，关于麻醉前评估与心功能评估，以下错误的是（）。

A.ASAⅣ级

B.ASAⅢ级

C.ASA急Ⅱ级

D.心功能Ⅱ级

E.心功能Ⅲ级

F.心功能Ⅳ级
查看答案
材料题

中新社北京2008年5月28日电中 * * * * 胡 * * 28日下午同中国国民党 * * 吴伯雄在北京人民大会堂举行了会谈。胡 * * 强调，在国共两党和两岸同胞共同努力下，台湾局势发生了积极变化，两岸关系发展面临着难得的历史机遇。这一局面来之不易，值得倍加珍惜。希望国共两党和两岸双方共同努力，建立互信、搁置争议、求同存异、共创双赢，继续依循并切实落实“两岸和平发展共同愿望”，以富有成效的努力，扎扎实实推动两岸关系不断取得实际进展，增强广大台湾同胞对两岸关系和平发展的信心。

从历史上看国共两党的关系变化经历了怎样的过程？请你查看相关资料，联系所学知识，想一想，国共两党最高领导人再次聚首有哪些重要意义？

________________________________________________________________________
查看答案