问题
问答题
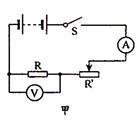
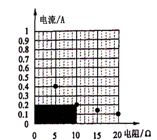
设函数φ(x)可导，且满足φ(0)=0，又φ’(x)单调减少．
(Ⅰ) 证明对x∈(0，1)，有φ(1)x＜φ(x)＜φ’(0)x；
(Ⅱ) 若φ(1)≥0，φ’(0)≤1，任取x0∈(0，1)，令xn=φ(xn-1)，n=1，2，…，证明
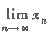存在，并求出该极限．
答案
参考答案：(Ⅰ) 方法1°当x∈(0，1)时φ(1)x＜φ(x)＜φ’(0)x[*]当x∈(0，1)时φ(1)[*]
考察[*]
其中x∈(0，1)，ξ∈(0，x)．由φ’(x)单调减少可得φ’(x)-φ’(ξ)＜0，因此[*]故[*]在(0，1]单调减少，从而当x∈(0，1)时有
[*]
于是φ(1)＜φ(x)＜φ’(0)x．
方法2°由于
φ(x)-φ’(0)x=[φ(x)-φ(0)]-φ’(0)x
=xφ’(ξ)-xφ’(0)=x[φ’(ξ)-φ’(0)]＜0，
其中x∈(0，1)，ξ∈(0，x)．因此有
φ(x)＜φ’(0)x (x∈(0，1))．
令F(x)=φ(x)-φ(1)x[*]F(x)可导，且F(0)=F(1)=0．由罗尔定理知[*]x0∈(0，1)，F’(x0)=0，又F’(x)=φ’(x)-φ(1)在(0，1)单调减少，于是
[*]
[*]F(x)＞0(x∈(0，1))，且φ(x)＞φ(1)x(x∈(0，1))．
(Ⅱ) xn∈(0，1)，由xn+1=φ(xn)＜φ’(0)xn≤xn知{xn}单调减少，又由
xn+1=φ(xn)＞φ(1)xn＞…＞φn+1(1)x0≥0
知{xn