问题
解答题
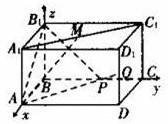
长方体ABCD-A1B1C1D1中,AB=4,AD=6,AA1=4,M是A1C1的中点,P在线段BC上,且CP=2,Q是DD1的中点,求:
(1)M到直线PQ的距离;
(2)M到平面AB1P的距离.
答案
如图,建立空间直角坐标系B-xyz,则A(4,0,0),M(2,3,4),P(0,4,0),Q(4,6,2).
(1)∵
=(-2,-3,2),QM
=(-4,-2,-2),QP
∴
在QM
上的射影为QP
=
•QM QP |
|QP
=(-2)×(-4)+(-3)×(-2)+2×(-2) (-4)2+(-2)2+(-2)2
,5 6 6
故M到PQ的距离为
=
2-(QM
)25 6 6
.462 6
(2)设
=(x,y,z)是平面AB1P的法向量,则n
⊥n
,AB1
⊥n
,AP
∵
=(-4,0,4),AB1
=(-4,4,0),AP
∴
.-4x+4z=0 -4x+4y=0
因此可取
=(1,1,1),由于n
=(2,-3,-4),MA
那么点M到平面AB1P的距离为d=
=|
•MA
|n |
|n
=|2×1+(-3)×1+(-4)×1| 3
,5 3 3
故M到平面AB1P的距离为
.5 3 3

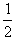 d,其他条件不变,这时两极板间电势差为U2,板间场强为E2,下列说法正确的是 [ ]
d,其他条件不变,这时两极板间电势差为U2,板间场强为E2,下列说法正确的是 [ ]