（1）取BC₁的中点H，连接HE、HF，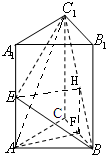

则△BCC₁中，HF∥CC₁且HF=

1

2

CC₁

又∵平行四边形AA₁C₁C中，AE∥CC₁且AE=

1

2

CC₁

∴AE∥HF且AE=HF，可得四边形AFHE为平行四边形，

∴AF∥HE，

∵AF⊄平面REC₁，HE⊂平面REC₁

∴AF∥平面REC₁．…（6分）

（2）等边△ABC中，高AF=

3

2

AB=

3

，所以EH=AF=

3

由三棱柱ABC-A₁B₁C₁是正三棱柱，得C₁到平面AA₁B₁B的距离等于

3

∵Rt△A₁C₁E≌Rt△ABE，∴EC₁=EB，得EH⊥BC₁

可得S_△BEC1=

1

2

BC₁•EH=

1

2

×

42+22

×

3

=

15

，

而S_△ABE=

1

2

AB×BE=2

由等体积法得V_A-BEC1=V_C1-BEC，

∴

1

3

S_△BEC1×d=

1

3

S_△ABE×

3

，（d为点A到平面BEC₁的距离）

即

1

3

×

15

×d=

1

3

×2×

3

，解之得d=

2 5

5

∴点A到平面BEC₁的距离等于

2 5

5

．…（12分）