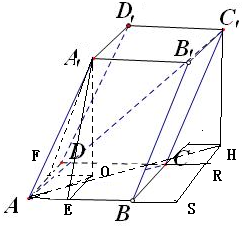
由题意，如图，作A₁O⊥底面于O，作OE垂直AB于E，OF垂直AD于F，连接A₁F，A₁E，

由于，∠BAA₁=∠DAA₁=60°，故有△A₁FA≌△A₁EA，即A₁F=A₁E

从而有△A₁FO≌△A₁EO，即有OF=OE，由作图知，O在角DAB的角平分线上，

又底面是矩形，故角DAO=角BAO=45°，

又AB=1，AD=2，AA₁=3，∠BAA₁=∠DAA₁=60°，

∴A₁F=A₁E=

3 3

2

，AE=AF=

3

2

，于是有AO=

3 2

2

，

在直角三角形A₁OA中，解得A₁O=

3 2

2

在图中作C₁H垂直底面于H，作HR垂直DC延长线与R，由几何体的性质知，HR=CR=

3

2

，A₁O=C₁H=

3 2

2

连接AH，得如图的直角三角形ASH，直角三角形AHC₁，由已知及上求解得AS=

5

2

，SH=

7

2

∴AC₁²=AH²+C₁H²=AS²+SH²+C₁H²=

25

4

+

49

4

+

18

4

=

92

4

=23

∴AC₁=

23

故答案为

23