问题
填空题
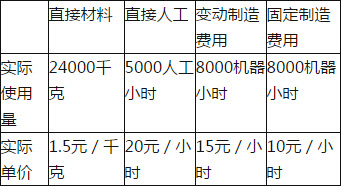
在120°的二面角α-l-β内有一点P,P在平面α、β内的射影A、B分别落在半平面αβ内,且PA=3,PB=4,则P到l的距离为______.
答案
∵在120°的二面角α-l-β内有一点P,
P在平面α、β内的射影A、B分别落在半平面αβ内,
∴∠APB=60°
又∵PA=3,PB=4,
∴AB=
=PA2+PB2-2PA•PB•cos∠APB
,13
而P到l的距离即为△PAB的外接圆直径,
由正弦定理得2R=
=AB sin∠APB
=13 3 2
,2 39 3
故答案为:
.2 39 3