∵三棱锥P-ABC中，PA、PB、PC两两互相垂直

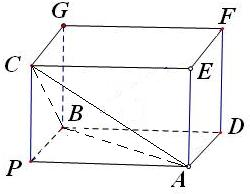
∴构造一个以PA、PB、PC为长宽高的长方体（如图）

三棱锥P-ABC的体积=

1

3

S△ABC×d（d为点P到平面ABC的距离）

三棱锥C-ABP的体积=

1

3

S△ABP×PC，

∵三棱锥P-ABC的体积=三棱锥C-ABP的体积，

∴

1

3

S△ABC×d=

1

3

S△ABP×PC，

则d=

2

2

，

则点P到平面ABC的距离为

2

2

故选：A