问题
填空题
已知三棱锥P-ABC的三条侧棱两两垂直,且分别长为2、4、4,则顶点P到面ABC的距离为______.
答案
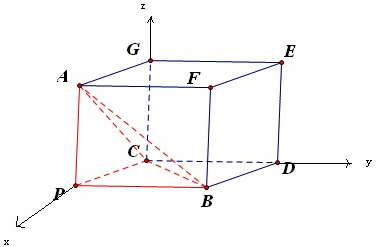
以PA、PB、PC为过同一顶点的三条棱,作长方体如图,
以CP为x轴,以CD为y轴,以CG为z轴,建立空间直角坐标系,
∵PA=2,PB=PC=4,
∴P(4,0,0),A(4,0,2),B(4,4,0),C(0,0,0),
∴
=(4,0,0),CP
=(4,0,2),CA
=(4,4,0),CB
设平面ABC的法向量
=(x,y,z),则n
•n
=0,CA
•n
=0,CB
∴
,解得4x+2z=0 4x+4y=0
=(1,-1,-2),n
∴顶点P到面ABC的距离d=
=|
•CP
|n |
|n
=|4+0+0| 1+1+4
.2 6 3
故答案为:
.2 6 3