问题
填空题
正四棱锥P-ABCD的所有棱长都相等,则侧棱与底面所成的角为 .
答案
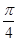
题目分析:根据题意,由于正四棱锥P-ABCD的所有棱长都相等,可知顶点在底面的射影为底面的中心,则可知侧棱长假设为2
高为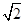 ,则可知侧棱与底面所成的角的正弦值为
,则可知侧棱与底面所成的角的正弦值为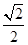 ,故可知角为
,故可知角为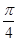
点评:解决的关键是根据线面角的定义,作出顶点在底面的射影,然后得到线面角,求解,属于基础题。
正四棱锥P-ABCD的所有棱长都相等,则侧棱与底面所成的角为 .
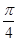
题目分析:根据题意,由于正四棱锥P-ABCD的所有棱长都相等,可知顶点在底面的射影为底面的中心,则可知侧棱长假设为2
高为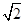 ,则可知侧棱与底面所成的角的正弦值为
,则可知侧棱与底面所成的角的正弦值为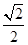 ,故可知角为
,故可知角为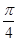
点评:解决的关键是根据线面角的定义,作出顶点在底面的射影,然后得到线面角,求解,属于基础题。