问题
解答题
已知ABCD是矩形,AD=2AB,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.
(Ⅰ)求证:DF⊥平面PAF;
(Ⅱ)在棱PA上找一点G,使EG∥平面PFD,当PA=AB=4时,求四面体E-GFD的体积.
答案
(Ⅰ)由矩形ABCD中,AD=2AB,点F是BC的中点,得到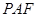 平面
平面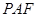 ;
;
(II)过 作
作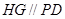 交
交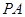 于
于 ,即为所求.
,即为所求. 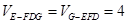 。
。
题目分析:(Ⅰ)在矩形ABCD中,因为AD=2AB,点F是BC的中点,
所以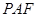 平面
平面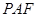 6分
6分
(II)再过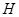 作
作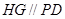 交
交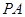 于
于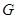 ,所以
,所以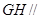 平面
平面 ,且
,且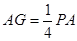 10分
10分
所以平面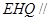 平面
平面 ,所以
,所以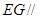 平面
平面 ,
,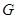 点即为所求.
点即为所求.
因为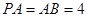 ,则
,则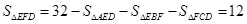 ,AG=1
,AG=1
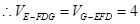 12分
12分
点评:简单题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤。利用向量可简化证明过程。(II)利用了“等积法”。
