问题
填空题
沿对角线AC将正方形ABCD折成直二面角后，则AC与BD所成的角等于_______
答案
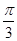
题目分析：如下图，取AC、BD、BC的中点依次为E、F、G，
连接BD、EF、EG、FG，
则FG∥CD，EG∥AB，
故∠FGE为异面直线AB与CD所成的角（或其补角），
设正方形的边长为2个单位，则FG=1，EG=1，EF=1，
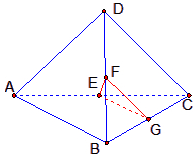
从而∠FGE=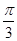，故答案为：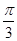
点评：利用三角形中位线定理，证明线FG∥CD，EG∥AB，结合异面直线夹角的定义，利用平移法构造∠FGE为异面直线AB与CD所成的角，是解答本题的关键．