若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则 (写出所有正确结论的编号).
①四面体ABCD每组对棱相互垂直;
②四面体ABCD每个面的面积相等;
③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°;
④连接四面体ABCD每组对棱中点的线段相互垂直平分;
⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.
②④⑤
把四面体补形为平行六面体,由三组对棱分别相等可知此平行六面体为长方体,如图所示,只有长方体为正方体时①才正确,故①不正确.
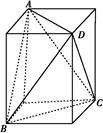
在长方体中,有△BAC≌△DCA.
△ABC≌△DCB,△CBD≌△ADB.
∴四面体ABCD每个面的面积都相等,故②正确.
对于③,以∠BAC,∠CAD,∠BAD为例说明.
∵△BAC≌△DCA,∴∠CAD=∠ACB.
又∵△DAB≌△CBA,
∴∠BAD=∠ABC.
∴∠BAC+∠CAD+∠BAD=∠BAC+∠ACB+∠ABC=180°,故③不正确.
对于④,连接四面体ABCD对棱中点的线段即是连接长方体对面中心的线段,显然相互垂直平分,故④正确.
对于⑤,以AB、AC、AD为例进行说明.
∵AD=BC,AB、AC、BC三边长可构成△ABC,
∴AB、AC、AD可以作为一个三角形的三边长.同理可得从其他顶点出发的三条棱的长也可以作为一个三角形的三边长.故⑤正确.

