（16分）如图，水平放置的平行板电容器，原来两极板不带电，上极板接地，它的极板长L＝0.1 m，两极板间距离d＝0.4 cm.有一束相同微粒组成的带电粒子流从两板中央平行于极板射入，由于重力作用微粒落到下板上．已知微粒质量为m＝2×10－6 kg，电荷量为q＝＋1×10－8 C，电容器电容为C＝10－6 F，g 取10 m/s2，求：
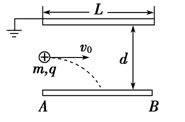
(1)为使第一个微粒的落点范围在下极板中点到紧靠边缘的B点之内，则微粒入射速度v0应为多少？
(2)若带电粒子落到AB板上后电荷全部转移到极板上，则以上述速度射入的带电粒子最多能有多少个落到下极板上？
(1) 2.5 m/s<v0<5 m/s(2)600个
(1)若第一个粒子落到O点，
由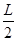
＝v01t1 ---------2分
＝
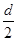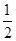
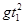得v01＝2.5 m/s ---------2分
若落到B点，由L＝v02t1 -------2分
＝
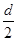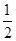
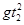得v02＝5 m/s
故 2.5 m/s<v0<5 m/s.-----------2分
(2)由L＝v01t，得t＝4×10－2 s--------2分
由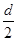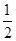＝ at2得a＝2.5 m/s2-------------2分
由mg －qE＝ma，E＝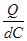
----------2分
得Q＝6×10－6C
所以n＝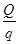
＝600个．----------2分
本题带电粒子在匀强电场中的偏转，如果粒子落在O点，由粒子所受电场力方向与速度方向垂直可知粒子做的是类平抛运动，由平抛运动规律可求得此时速度大小，如果粒子落在B点，由水平和竖直方向的分运动可求得此时速度大小，由此可知粒子初速度的取值范围，随着落在下极板的电荷越来越多，极板间的场强越来越大，由水平分速度先求的运动时间，再由竖直方向的匀加速直线运动求得加速度大小，由牛顿第二定律求得电场力大小，由E=U/d可求得电压大小，由电容器的电容公式可求得极板带电量，从而求得粒子个数