问题
选择题
在四棱锥P—ABCD中，底面ABCD是正方形，侧棱PD⊥平面ABCD，AB＝PD＝a．点E为侧棱PC的中点，又作DF⊥PB交PB于点F．则PB与平面EFD所成角为( )
A．30°
B．45°
C．60°
D．90°
答案
答案：D
建立空间直角坐标系D—xyz，D为坐标原点．P(0，0，a)，B(a，a，0)，
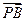＝(a，a，－a)，又
＝
，
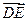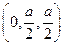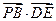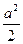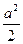＝0＋
－＝0，
所以PB⊥DE．由已知DF⊥PB，又DF∩DE＝D，
所以PB⊥平面EFD，所以PB与平面EFD所成角为90°，选D．