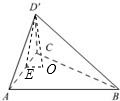
设面ACD′为α，面ABC为β，取AC的中点E，连接D′E，再过D′作D′O⊥β，垂足为O，连接OE，则D′E⊥AC

∵AC⊥D′E，∴AC⊥OE

∴∠D′EO为二面角a-AC-β的平面角，∴∠D′EO=60°

在直角梯形ABCD中，由已知△DAC为等腰直角三角形，

∴AC=

2

，∠CAB=45°，∴D′E=

1

2

AC=

2

2

，

在直角△D′OE中，D′E=

2

2

，∴D′O=

6

4

∴VD-ABC=

1

3

S△ABC•D′O=

1

3

×

1

2

AC•BC•D′O=

1

6

×

2

×

2

×

6

4

=

6

12

．

故答案为：

6

12