在(2x-3y)10的展开式中,求:
(1)二项式系数的和;
(2)各项系数的和;
(3)奇数项的二项式系数和与偶数项的二项式系数和;
(4)奇数项系数和与偶数项系数和;
(5)x的奇次项系数和与x的偶次项系数和.
(1) 210 (2) 1(3) 29(4)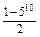 (5)
(5)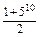
设(2x-3y)10=a0x10+a1x9y+a2x8y2+…+a10y10 (*)
各项系数和即为a0+a1+…+a10,奇数项系数和为a0+a2+…+a10,偶数项系数和为a1+a3+a5+…+a9,x的奇次项系数和为a1+a3+a5+…+a9,x的偶次项系数和a0+a2+a4+…+a10.
由于(*)是恒等式,故可用“赋值法”求出相关的系数和.
(1)二项式系数和为C +C
+C +…+C
+…+C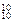 =210.
=210.
(2)令x=y=1,各项系数和为(2-3)10=(-1)10=1.
(3)奇数项的二项式系数和为C +C
+C +…+C
+…+C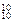 =29,
=29,
偶数项的二项式系数和为C +C
+C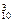 +…+C
+…+C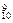 =29.
=29.
(4)设(2x-3y)10=a0x10+a1x9y+a2x8y2+…+a10y10
令x=y=1,得到a0+a1+a2+…+a10="1 " ①
令x=1,y=-1(或x=-1,y=1)
得a0-a1+a2-a3+…+a10=510 ②
①+②得2(a0+a2+…+a10)=1+510,
∴奇数项的系数和为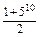 ;
;
①-②得2(a1+a3+…+a9)=1-510,
∴偶数项的系数和为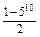 .
.
(5)x的奇次项系数和为a1+a3+a5+…+a9=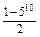 ;
;
x的偶次项系数和为a0+a2+a4+…+a10=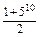 .
.

 NaCl(l)+K(g)-Q 该反应的平衡常数可表示为:K=C(K)各物质的沸点与压强的关系见下表。
NaCl(l)+K(g)-Q 该反应的平衡常数可表示为:K=C(K)各物质的沸点与压强的关系见下表。