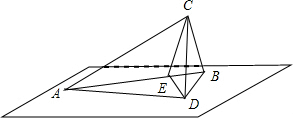
从C向平面作垂线CD，连接AD，BD，作CE⊥AB，连接DE，

根据三垂线定理，DE⊥AB，设CD=h，∠CBD=45°，BC=

2

h，∠CAD=30°，AC=2CD=2h，

∠CED是二面角的平面角，∠CED=60°，CE=

2 3 h

3

，

根据勾股定理，AE=

2 6

3

h，BE=

6

3

h，AB=AE+BE=

6

h，

∵（

6

h）²=（

2

h）²+（2h）²，即AB²=BC²+AC²，

∴∠C=90°，sinC=1，

另一种是∠B是钝角，CE在三角形ABC之外，AB=AE-BE=

6 h

3

，

根据余弦定理，AB²=AC²+BC²-2AC×BC×cosC，

（

6

3

h）²=（2h）²+（

2

h）²-2×2h×

2

hcosC，

cosC=

2 2

3

，

sinC=

1-cos2C

=

1

3

，

故角ACB的正弦值是1或

1

3

．

故选D．