问题
填空题
将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:
(1)AC⊥BD;
(2)△ACD是等边三角形
(3)AB与平面BCD所成的角为60°;
(4)AB与CD所成的角为60°.
则正确结论的序号为______.
答案
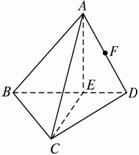
取BD的中点E,则AE⊥BD,CE⊥BD.∴BD⊥面AEC.
∴BD⊥AC,故(1)正确.
设正方形边长为a,则AD=DC=a,AE=
a=EC.2 2
∴AC=a.
∴△ACD为等边三角形,故(2)正确.
∠ABD为AB与面BCD所成的角为45°,故(3)不正确.
以E为坐标原点,EC、ED、EA分别为x,y,z轴建立直角坐标系,
则A(0,0,
a),B(0,-2 2
a,0),D(0,2 2
a,0),C(2 2
a,0,0).2 2
=(0,-AB
a,-2 2
a),2 2
=(DC
a,-2 2
a,0).2 2
cos<
,AB
>=DC
=
a21 2 a2 1 2
∴<
,>=60°,故(4)正确.AB
故答案为:(1),(2),(4)
