问题
解答题
正方体ABCD﹣A1B1C1D1的棱长为a．求：
（1）二面角A﹣BD﹣A1的正切值；
（2）AA1与平面A1BD所成的角的余弦值．
答案
解：（1）连接AC，AC∩BD=O，
连接A1O，则∠A1OA为二面角A﹣BD﹣A1的平面角
∵正方体ABCD﹣A1B1C1D1的棱长为a，
∴AO=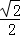
a
∴tan∠A1OA=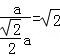
；
（2）过A作AE⊥A1O，垂足为E，
∵AE⊥BD，A1O∩BD=O，
∴AE⊥平面A1BD
∴∠AA1O为AA1与平面A1BD所成的角
∵A1A=a，AO=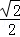
a
∴A1O=
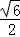a
∴AA1与平面A1BD所成的角的余弦值为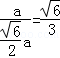
．
