(18分)如右图所示,匀强电场E=4V/m,方向水平向左,匀强磁场 B=2T,方向垂直纸面向里。m=1g带正电的小物块A,从M点沿绝缘粗糙的竖直壁无初速下滑,它滑行0.8m到N点时就离开壁做曲线运动,在P点A瞬时受力平衡,此时其速度与水平方向成45°角。设P与M的高度差为1.6m。(g取10m/s2) 求:
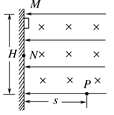
(1)A沿壁下滑时摩擦力做的功;
(2)P与M的水平距离。
(1)6×10-3J (2)0.6m
(1)从M→N过程,只有重力和摩擦力做功.刚离开N点时有 Eq=Bqv
即v=E/B=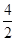 m/s=2m/s.
m/s=2m/s.
根据动能定理mgh-Wf=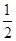 mv2
mv2
所以Wf=mgh+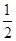 mv2=1×10-3×10×0.8-
mv2=1×10-3×10×0.8-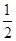 ×1×10-3×22=6×10-3(J).
×1×10-3×22=6×10-3(J).
(2)从已知P点速度方向及受力情况分析如下图
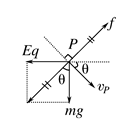
由θ=45°可知 mg=Eq
f洛=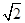 mg=Bqvp
mg=Bqvp
所以vP=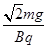 =
=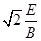 =2
=2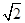 m/s.
m/s.
根据动能定理,取M→P全过程有 mgH-Wf-Eqs=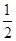
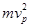
求得最后结果s=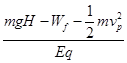 =0.6m.
=0.6m.
本题考查带电粒子在复合场中的运动,离开竖直墙面时弹力等于零,分析受力可知,此时的电场力等于洛仑兹力,由此求得此时的速度大小,在运动过程中,有重力和阻力做功,根据动能定理可求得克服阻力做功,再以P点分析,由于在P点受力平衡可以判断电场力与重力的合力、洛仑兹力的关系是等大反向的,根据洛仑兹力公式可判断此时速度大小,由M到P点应用动能定理可求得位移s
点评:复合场的问题一直是高考的热点,分析受力、做功和某一个状态是解决此类问题的关键,本题中随着物体速度的变化洛仑兹力也在发生变化,物体不是匀变速运动,这是学生容易忽视的问题
