问题
解答题
设m，n∈N*，f(x)＝(1＋2x)m＋(1＋x)n.
(1)当m＝n＝2 011时，记f(x)＝a0＋a1x＋a2x2＋…＋a2 011x2 011，求a0－a1＋a2－…－a2 011；
(2)若f(x)展开式中x的系数是20，则当m，n变化时，试求x2系数的最小值．
答案
（1）-1（2）85
(1)令x＝－1，得a0－a1＋a2－…－a2 011＝(1－2)2 011＋(1－1)2 011＝－1.
(2)因为2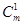
＋
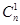＝2m＋n＝20，所以n＝20－2m，则x2的系数为22
＋
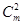＝4×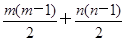
＝2m2－2m＋
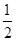(20－2m)(19－2m)＝4m2－41m＋190.
所以当m＝5，n＝10时，f(x)展开式中x2的系数最小，最小值为85.