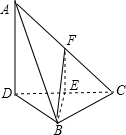
由已知可得AD⊥DC

又由其余各棱长都为1得正三角形BCD，取CD得中点E，连BE，则BE⊥CD

在平面ADC中，过E作AD的平行线交AC于点F，则∠BEF为二面角A-CD-B的平面角

∵EF=

1

2

（三角形ACD的中位线），BE=

3

2

（正三角形BCD的高），BF=

2

2

（等腰RT三角形ABC，F是斜边中点）

∴cos∠BEF

EF2+BE2-BF2

2×BE×EF

=

1 4 + 3 4 - 1 2

2× 3 2 × 1 2

=

3

3

故选C．