问题
计算题
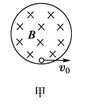
（16分）在竖直平面内有一圆形绝缘轨道，半径为R＝0.4m，匀强磁场垂直于轨道平面向里，一质量为m＝1×10－3kg、带电量为q＝＋3×10－2C的小球，可在内壁滑动，如图甲所示，开始时，在最低点处给小球一个初速度v0，使小球在竖直平面内逆时针做圆周运动，如图乙(a)是小球在竖直平面内做圆周运动的速率v随时间变化的情况，图乙(b)是小球所受轨道的弹力F随时间变化的情况，结合图象所给数据，(取g＝10m/s2) 求：
（1）磁感应强度的大小；
（2）初速度v0的大小。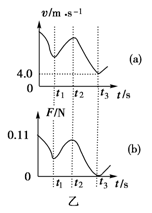
答案
(1)0.25T (2)8m/s
(1)从乙图(a)可知，小球第二次到达最高点时，速度大小为4m/s，而由乙图(b)知，此时轨道与球间的弹力为零，故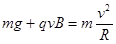
代入数据得：B=0.25T
(2)从图乙可知，小球最初在最低点时，轨道与球之间的弹力为F=0.11N，根据牛顿第二定律得：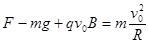
代入数据得：v0=8m/s
本题考查带电粒子在磁场中的偏转，在圆周运动中无论小球运动到哪个位置，沿着半径方向的合力提供向心力，结合图像分析a图中小球第二次到达最高点时速度为4m/s，分析受力列公式求解，同理分析乙图最初在最低点时，轨道的弹力最大，列公式求解
点评：本题利用图像传递着速度和支持力的一些信息，把两个图结合来看是本题的关键，圆周运动中沿着半径方向的合力提供向心力，分析步骤：进行受力分析、把不在半径方向的力分解后进行合成、根据沿着半径方向的力提供向心力