问题
填空题
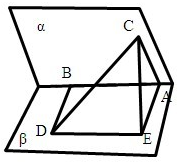
已知二面角α-AB-β为120°,AC⊂α,BD⊂β,且AC⊥AB,BD⊥AB,AB=AC=BD=a,则CD的长为______.
答案
由题意,作出如图的图象,在平面β中可过A作AB的垂线,过D作BD的垂线,两者交于E连接CE,
由作图知,四边形ABDE是矩形,故有DE=AB=a,AE=BD=a,AE⊥AB
又AC⊥AB,易得AB⊥面ACE,即有CE⊥AB,进而得CE⊥DE
有二面角的平面角的定义知,∠CAE=120°
在△CAE中,由余弦定义可得CE2=a2+a2-2×a2×(-
)=3a2,故CE=1 2
a3
在直角三角形CED中,由勾股定理得CD2=DE2+CE2=a2+3a2=4a2,
可得CD的长为2a
故答案为:2a.