问题
填空题
设(2x-1)6=a6x6+a5x5+…+a1x+a0,则|a0|+|a1|+|a2|+…+|a6|=________.
答案
729
∵Tr+1=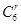 (2x)6-r(-1)r=(-1)r26-r
(2x)6-r(-1)r=(-1)r26-r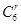 x6-r,
x6-r,
∴ar+1=(-1)r26-r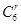 ,
,
∴|a0|+|a1|+|a2|+…+|a6|
=a0-a1+a2-a3+a4-a5+a6
=[2×(-1)-1]6=36=729.
设(2x-1)6=a6x6+a5x5+…+a1x+a0,则|a0|+|a1|+|a2|+…+|a6|=________.
729
∵Tr+1=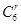 (2x)6-r(-1)r=(-1)r26-r
(2x)6-r(-1)r=(-1)r26-r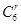 x6-r,
x6-r,
∴ar+1=(-1)r26-r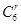 ,
,
∴|a0|+|a1|+|a2|+…+|a6|
=a0-a1+a2-a3+a4-a5+a6
=[2×(-1)-1]6=36=729.