问题
填空题
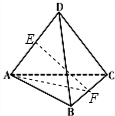
边长为4的正四面体P-ABC中,E为PA的中点,则平面EBC与平面ABC所成锐二面角的余弦值为______.
答案
取BC的中点F,连接EF,AF,
∵四面体P-ABC为正四面体,
∴EF⊥BC,AF⊥BC,
∴∠EFA为平面EBC与平面ABC所成锐二面角,
∵边长为4,E为PA的中点,
∴EA=2,AF=2
,EF⊥AP,3
∴EF=
=2(2
)2-43
,2
∴cos∠EFA=
=EF AF
=2 2 2 3
,6 3
故答案为:
.6 3