问题
解答题
(1)已知(1－2x)2008＝a0＋a1x＋a2x2＋…＋a2008x2008(x∈R)，求a0＋a1＋a2＋…＋a2008的值；
(2)已知(1－2x＋3x2)7＝a0＋a1x＋a2x2＋…＋a13x13＋a14x14，求a1＋a3＋a5＋…＋a13的值．
答案
(1)1 (2)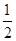
(27－67)
解：(1)令x＝1，则(1－2x)2008＝a0＋a1x＋a2x2＋…＋a2008x2008变为(1－2)2008＝a0＋a1＋a2＋…＋a2008，
∴a0＋a1＋a2＋…＋a2008＝1.
(2)分别令x＝1及x＝－1，
可得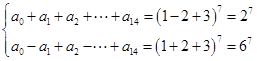
两式相减，用上式减下式可得
2(a1＋a3＋…＋a13)＝27－67，
∴a1＋a3＋a5＋…＋a13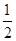＝ (27－67)．