正四面体ABCD边长为2，AO⊥平面BCD，垂足为O，设M为线段AO上一点_爱下问搜题

搜题请搜索小程序“爱下问搜题”

问题填空题

正四面体ABCD边长为2，AO⊥平面BCD，垂足为O，设M为线段AO上一点，且∠BMC=90°，则二面角M-BC-O的余弦值为______．

答案

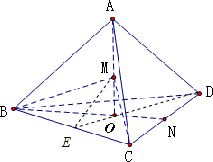
延长BO，交CD于点N，可得BN⊥CD且N为CD中点．

设正四面体ABCD棱长为1，得等边△ABC中，BN=

3

2

∵AO⊥平面BCD，

∴O为等边△ABC的中心，得BO=

2

3

BN=

3

3

Rt△ABO中，AO=

6

3

设MO=x，则Rt△BOM中，BM=

1

3

+x2

∵∠BMC=90°，得△BMC是等腰直角三角形，

∴BM=AM=

2

2

BC

∴

1

3

+x2

=

2

2

∴MO=

6

6

延长DO，交BC于点E，则DE⊥BC且E为BC中点，连接ME，则∠MEO是二面角M-BC-O的平面角

∵MO=

6

6

，OE=

3

6

∴ME=

(

6

6

)2+(

3

6

)2

=

1

2

∴cos∠MEO=

OE

ME

=

3

3

故答案为

3

3

．

填空题

腰穿检查做压颈试验时，压颈10s压力不升，提示___________；压颈上升较快，解除压颈后下降缓慢，或上升慢下降更慢，提示___________，压迫一侧颈静脉，压力不升，压迫对侧上升正常，提示_______________。

判断题

对于一组试验数据进行异常值检验，格拉布斯法和狄克逊法可以任选一种进行。