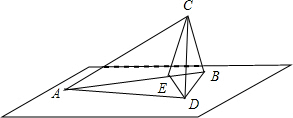
过点C作CD⊥平面α，设CD=h，

∵AC，BC与平面α分别成30°，45°的角，

∴BC=

2

h，AC=2h，AB=

6

h，

∵直角三角形ABC的斜边AB在平面α内，

S_△=

1

2

BC?AC=10，∴h=

5 2

，

设直角三角形ABC的斜边AB上的高为x，

由面积法可求 x=

2

3

15 2

，

设直角三角形ABC与平面α成的角为β，

sinβ=

h

x

=

3

2

，∴β=60⁰，

故答案为60⁰．