问题
填空题
已知三棱锥A-BCD的体积是V,棱BC的长是a,面ABC和面DBC的面积分别是S1和S2.设面ABC和面DBC所成的二面角是α,那么sinα=______.
答案
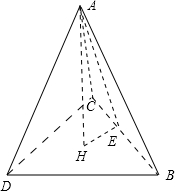
如图,过顶点A向底面BCD作AH⊥平面BCD,
在平面ABC内作AE⊥BC,连结HE,
根据三垂线定理可知,HE⊥BC,
所以∠AEH是二面角A-BC-D的平面角,则∠AEH=α,
由已知S△BCD=S2,三棱锥A-BCD的体积为V=
S2•AH,AH=1 3
,3V S2
S△ABC=S1=
AE•BC,AE=21 2
,S1 a
sinα=
=AH AE
=3V S2 2S1 a
.3aV 2S1S2
所以面ABC和面DBC所成二面角的正弦值为
.3aV 2S1S2
故答案为
.3aV 2S1S2

 ()
()